This paper presents a prediction algorithm for estimating the upper bound of future Web traffic volume. Unlike traditional traffic predictions that are performed at a single time scale using curve fitting, we employ a multiple time scale approach and utilize traffic statistical properties to do forecasting. We have applied our prediction algorithm to the 1998 World Cup data set. Experiments show that it is effective for short term traffic bound predictions, applicable to bursty traffic, and useful for Web server overload prevention.
Traffic prediction, upper bound, multiple time scale approach, self-similar, overload prevention.
To provide expected quality of services, a Web site needs to predict its future traffic volume: long term predictions (e.g., in months or years) are useful for capacity planning, while short term predictions (e.g., in seconds or minutes) are useful for overload prevention.
As Web has a large number of potential users, a Web site may receive highly bursty requests and get overwhelmed, which is known as the flash crowd phenomenon. When a Web server becomes overloaded, its service quality will be seriously degraded: its users will perceive longer delays or even lose services. To prevent overload, capacity planning is not sufficient since the real traffic volume may exceed the planned capacity. Moreover, provisioning according to the peak traffic volume or even over-provisioning is not cost effective since Web traffic has a large variance. To better handle overload, dynamic load shedding and migration are needed, such as the Hotspot Rescue Service [2]. Short term traffic predictions are important for a server to take needed actions in advance when it anticipates an approaching peak load which is likely to exceed its capacity or a preset threshold.
Note that for overload prevention, we only need to predict an upper bound of the future traffic volume. More precisely, whether the future traffic volume will exceed the server's capacity or a preset threshold. As long as the future traffic volume is below the predicted bound, the exact volume does not matter much here. Also note that for overload prevention, over-prediction has a less penalty than under-prediction because a false alarm only incurs unnecessary overheads, but a miss prediction of an excess traffic can cause the server being overloaded.
In this paper, we describe a prediction algorithm for estimating the upper bound of future Web traffic volume. We employ a multiple time scale approach by using traffic information at a smaller time scale to forecast traffic volume at a larger time scale. Furthermore, we utilize traffic statistical properties other than curve fitting to do forecasting. The rest of this paper is organized as follows: we give the motivation in Section 2, describe our prediction algorithm in Section 3, discuss the parameter selection in Section 4, present experiment results in Section 5, and conclude in Section 6.
Traditionally, traffic predictions are carried at a single time scale
using curve fitting. A difficult issue here is to choose the right number
(denoted as ![]() ) of history intervals used for predictions: if
) of history intervals used for predictions: if
![]() is too large, then predictions are
based upon less relevant information in history, whereas if
is too large, then predictions are
based upon less relevant information in history, whereas if
![]() is too small, then predictions are made from incomplete
information; both cases lead to poor predictions. Usually
better predictions can be achieved by varying
is too small, then predictions are made from incomplete
information; both cases lead to poor predictions. Usually
better predictions can be achieved by varying ![]() dynamically,
but it is hard to derive the correct
dynamically,
but it is hard to derive the correct ![]() .
.
To avoid the trouble of choosing ![]() , we seek a new approach to
traffic predictions by only using traffic information in current interval.
More specifically, we try to correlate how traffic changes within current
interval at a smaller time scale (e.g., one tenth of current time scale)
with that at current time scale. Previous work on self similarity
[3] has shown that statistical correlations
exist for Web traffic at different time scales. From a first look, it seems
that self similarity is not useful for traffic predictions since it is a
property for stationary processes, whereas predictions are more useful when
traffic volume changes quickly and dramatically. A careful re-consideration
reveals that no matter how quickly a traffic changes, at sufficiently small
time scales, the change between adjacent intervals will be small. Equivalently,
we can regard the mean of traffic volume in adjacent intervals as unchanged
and the real change as variability. Note that for three consecutive intervals:
, we seek a new approach to
traffic predictions by only using traffic information in current interval.
More specifically, we try to correlate how traffic changes within current
interval at a smaller time scale (e.g., one tenth of current time scale)
with that at current time scale. Previous work on self similarity
[3] has shown that statistical correlations
exist for Web traffic at different time scales. From a first look, it seems
that self similarity is not useful for traffic predictions since it is a
property for stationary processes, whereas predictions are more useful when
traffic volume changes quickly and dramatically. A careful re-consideration
reveals that no matter how quickly a traffic changes, at sufficiently small
time scales, the change between adjacent intervals will be small. Equivalently,
we can regard the mean of traffic volume in adjacent intervals as unchanged
and the real change as variability. Note that for three consecutive intervals:
![]() ,
, ![]() , and
, and ![]() , we can view that
, we can view that ![]() and
and ![]() have
the same mean
have
the same mean ![]() , and
, and ![]() and
and ![]() have the same mean
have the same mean
![]() ; but
; but ![]() and
and ![]() can be unequal (i.e.,
can be unequal (i.e.,
![]() and
and ![]() can have different means). In this way, we can perform
predictions by utilizing self similarity within two adjacent intervals at
sufficiently small time scales. A good fit here is that self similarity is
measured in terms of statistical correlations between two different time
scales, which are just what we need to predict the upper bound of future
traffic volume.
can have different means). In this way, we can perform
predictions by utilizing self similarity within two adjacent intervals at
sufficiently small time scales. A good fit here is that self similarity is
measured in terms of statistical correlations between two different time
scales, which are just what we need to predict the upper bound of future
traffic volume.
We formulate our prediction problem as follows: given a time scale
![]() (such as
(such as ![]() seconds), we want to predict the upper bound of traffic
volume in next interval based on traffic information in current interval.
Note that the length of each interval is
seconds), we want to predict the upper bound of traffic
volume in next interval based on traffic information in current interval.
Note that the length of each interval is ![]() . Let
. Let ![]() and
and ![]() denote the traffic volume in current interval (
denote the traffic volume in current interval (![]() ) and next interval
(
) and next interval
(![]() ), respectively, and
), respectively, and ![]() denote the difference between
denote the difference between
![]() and
and ![]() (i.e.,
(i.e.,
![]() ). If we can find an
upper bound (denoted as
). If we can find an
upper bound (denoted as ![]() ) of
) of ![]() , then we can estimate that
, then we can estimate that
![]() .
In other words, predicting an upper bound for
.
In other words, predicting an upper bound for
![]() is equivalent to estimating
is equivalent to estimating ![]() . Next we show using statistical properties and self
similarity to estimate
. Next we show using statistical properties and self
similarity to estimate ![]() .
.
Let random variable ![]() denote the difference of traffic volume
between adjacent intervals at time scale
denote the difference of traffic volume
between adjacent intervals at time scale ![]() , and
, and ![]() and
and ![]() denote the mean and standard deviation of
denote the mean and standard deviation of ![]() , respectively.
If assuming that
, respectively.
If assuming that ![]() follows normal distribution, we can estimate
the bound of
follows normal distribution, we can estimate
the bound of ![]() using
using ![]() and
and ![]() . For example,
since about
. For example,
since about ![]() samples of
samples of ![]() fall into the range of
fall into the range of
![]() , we can say that
a sample of
, we can say that
a sample of ![]() will be less than
will be less than
![]() with more
than
with more
than ![]() probability.
In order to derive
probability.
In order to derive ![]() , we divide
, we divide ![]() into
into ![]() equal sub-intervals
with length of
equal sub-intervals
with length of ![]() , and look at
, and look at ![]() in these
in these
![]() intervals. With a sufficient number of samples
(e.g.,
intervals. With a sufficient number of samples
(e.g., ![]() ),
we can have an estimation for
),
we can have an estimation for ![]() and
and ![]() . If assuming that the traffic is self-similar
with Hurst parameter
. If assuming that the traffic is self-similar
with Hurst parameter ![]() within the period of
within the period of ![]() and
and ![]() , then we have
, then we have
![]() , and
, and
![]() .
With
.
With ![]() and
and ![]() , we can estimate
, we can estimate ![]() as
as
![]() . Note that here we choose
. Note that here we choose
![]() rather than
rather than
![]() mainly because we want to have
a closer upper bound estimation to avoid unnecessary false alarms.
Also note that since our prediction is based on statistical properties,
the predicted upper bound is correct only with a high probability.
mainly because we want to have
a closer upper bound estimation to avoid unnecessary false alarms.
Also note that since our prediction is based on statistical properties,
the predicted upper bound is correct only with a high probability.
Several parameters affect the prediction performance. The first
one is the prediction interval ![]() . As we use self similarity
to derive statistical correlations between two different time scales,
the mean of traffic volume should be roughly unchanged within the
period of
. As we use self similarity
to derive statistical correlations between two different time scales,
the mean of traffic volume should be roughly unchanged within the
period of ![]() . Usually
. Usually ![]() should not exceed
should not exceed ![]() seconds.
The second parameter is the scaling factor
seconds.
The second parameter is the scaling factor ![]() between the two
different time scales
between the two
different time scales ![]() and
and ![]() . As this parameter
decides the number of samples in time scale
. As this parameter
decides the number of samples in time scale ![]() used for deriving
statistical properties,
used for deriving
statistical properties, ![]() should be no less than
should be no less than ![]() . The third
one is the Hurst parameter
. The third
one is the Hurst parameter ![]() . Since we do not know the correct
. Since we do not know the correct ![]() in advance, and using a larger
in advance, and using a larger ![]() tends to over estimate whereas using
a smaller
tends to over estimate whereas using
a smaller ![]() tends to under estimate, the general guidances are as
follows: (1) the burstier the traffic, the larger
tends to under estimate, the general guidances are as
follows: (1) the burstier the traffic, the larger ![]() [4];
(2) a right
[4];
(2) a right ![]() will result in roughly the same prediction performance
when
will result in roughly the same prediction performance
when ![]() changes; and (3) use a little bit larger
changes; and (3) use a little bit larger
![]() if not sure,
usually in the range of
if not sure,
usually in the range of ![]() .
.
To evaluate our prediction algorithm, we apply it
to the 1998 World Cup data set [1], which includes
![]() billion requests made to
billion requests made to ![]() servers at four different regions
during a period of
servers at four different regions
during a period of ![]() days. We run our prediction algorithm for three servers
on three days. The three chosen servers are server5, server41 and server64,
which are selected from three different regions since servers in the same
region have very similar traffic curves. The three chosen days are June 29
(day65), July 7 (day73) and July 8 (day74), which are among the busiest
days in the data set. In each day, we choose a period of three hours that
includes a dramatic traffic spike.
days. We run our prediction algorithm for three servers
on three days. The three chosen servers are server5, server41 and server64,
which are selected from three different regions since servers in the same
region have very similar traffic curves. The three chosen days are June 29
(day65), July 7 (day73) and July 8 (day74), which are among the busiest
days in the data set. In each day, we choose a period of three hours that
includes a dramatic traffic spike.
We carry experiments in three steps. For preparation, we calculate
the number of requests at the following time scales (in second):
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
In different experiments, we vary
.
In different experiments, we vary ![]() ,
, ![]() and
and ![]() to evaluate
their effects on predictions. After each experiment, we calculate
the percentage of prediction intervals in which the real traffic
volume fall below the predicted upper bound.
to evaluate
their effects on predictions. After each experiment, we calculate
the percentage of prediction intervals in which the real traffic
volume fall below the predicted upper bound.
In the first experiment, we fix ![]() and
and ![]() , but vary
, but vary ![]() from
from ![]() to
to ![]() seconds. We get consistent prediction performance
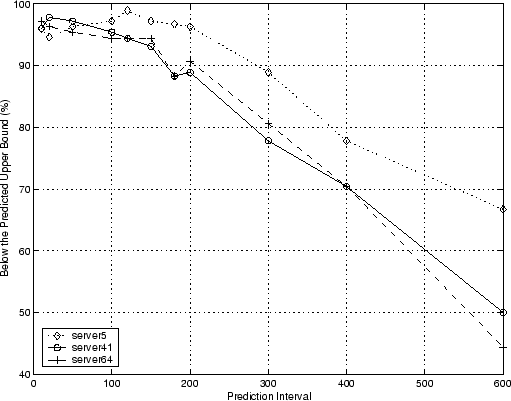
across all nine different server-day combinations. For clarity, we only
show the results for the three servers on day74 in
Figure 1. As we anticipate,
prediction performance changes as
seconds. We get consistent prediction performance
across all nine different server-day combinations. For clarity, we only
show the results for the three servers on day74 in
Figure 1. As we anticipate,
prediction performance changes as ![]() increases: around
increases: around ![]() when
when ![]() seconds, slowly degraded to around
seconds, slowly degraded to around ![]() when
when
![]() seconds, and down quickly when
seconds, and down quickly when ![]() seconds. We show the detailed
prediction results for server41 on day65 in
Figure 2.
seconds. We show the detailed
prediction results for server41 on day65 in
Figure 2.
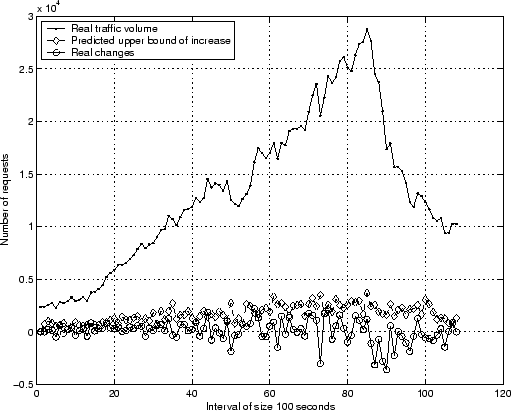
Since the finest time scale in the data set is ![]() second, and a good
prediction interval
second, and a good
prediction interval ![]() seconds, we have
seconds, we have
![]() .
In the second experiment, we fix
.
In the second experiment, we fix ![]() and
and ![]() , but vary
, but vary ![]() .
We predict using
.
We predict using
![]() , respectively, and get roughly the same
results. For example, for server41 on day65, the three predictions using
, respectively, and get roughly the same
results. For example, for server41 on day65, the three predictions using
![]() all have a
all have a ![]() performance, while the prediction using
performance, while the prediction using
![]() has a
has a ![]() performance with just one more miss prediction. This
validates that with a right
performance with just one more miss prediction. This
validates that with a right ![]() , predictions using different
, predictions using different ![]() (within
a certain range) are roughly equivalent, and that
(within
a certain range) are roughly equivalent, and that ![]() appears to be
the right value for this data set.
appears to be
the right value for this data set.
In the last experiment, we fix ![]() , but vary
, but vary ![]() and
and ![]() . This is
to determine a right
. This is
to determine a right ![]() based on the following property: increasing
based on the following property: increasing
![]() will raise the prediction performance if we are using a larger
will raise the prediction performance if we are using a larger
![]() , but
lower the prediction performance if we are using a smaller
, but
lower the prediction performance if we are using a smaller
![]() .
.
In this paper, we described a prediction algorithm for estimating the upper bound of future Web traffic volume, in which we employ a multiple time scale approach and utilize traffic statistical properties to do forecasting. We evaluated three algorithm parameters and showed that our algorithm is simple, effective for short term traffic bound predictions, applicable to bursty traffic, and useful for Web server overload prevention.
The work described in this paper was supported in part by the National Science Foundation under Grant No. ANI-0117738. Any opinions, findings, and conclusions or recommendations expressed in this paper are those of the authors and do not necessarily reflect the views of the National Science Foundation.